Many companies have improved since 2006, but you can help by critiquing those that have not. It is especially important to critique catalogs or websites that sell products for activities heretofore commonly thought of as “white,” such as river cruising, hiking, or classical music. Otherwise, the company contributes to stereotyping activities as “white” or “black” or maybe “Latinx.”
Use the photograph as your unit of analysis. Thus even if a photograph has 20 people in it, it just counts as one. If all the people are white, then it counts as one white photo. If at least one person is black, then it counts as one black photo. I also count Asians and Latinx. How do I decide Latinx? If they have black hair and “look” Latinx. Yes, I know I may be wrong, but in a way it doesn’t matter, because we’re not trying to be accurate. Rather, we want to record our shallow impression. If a person strikes me as likely Latinx, then that’s how s/he comes across. If this worries you, then ask a couple of your friends, preferably of different racial and ethnic backgrounds, to categorize the images too. You can also use “indeterminate” as a category.
When you have finished, you have, say, 115 images that include people. (Be sure to include body parts, such as a hand pushing a doorbell, for a company selling doorbells.) Suppose 100 show whites only, 8 include African Americans, 5 are likely Latinx, and 2 include Asians. Is that discriminatory? Only statistics can tell us.
Discriminatory compared to what? The simplest comparison group would be the national population. After all, it’s a national catalog, right? You may have good reason for using a different comparison group. For instance, a product may appeal only to the young, so the proportions of each race in the young population might be more appropriate. However, I generally would use the general population. After all, babies don’t buy diapers. Adults do.
In 2020, the national population was 62% non-Hispanic white, 13.5% black, 6.5% Asian, 1.3% Native American Indian, and 18.5% Hispanic. (Hispanics can be of any race, so it’s tricky to calculate these percentages. Also tricky: deciding what to do with multi-racial persons. That’s also why the population can add to more than 100 %.)
Your catalog is 87% non-Hispanic white, 7% black, 1.7% Asian, o% Native, and 4.3% Hispanic. Use the “difference of two proportions” statistical test to see whether 13.5% is significantly different from 7%. We can assume that the proportion black in the population won’t vary, because it’s not a sample; we have the actual percentage in the underlying population. (Yes, the census is imperfect, but that’s not at issue here.) However, the proportion black in the catalog might vary. We don’t have the complete population of all photos used in all the catalogs in recent years. So we need to calculate the “standard error” of our proportion black of .07. The formula is intuitively clear: we subtract the smaller proportion from the larger proportion and compare the difference to what is called the “standard error of the proportion.” .135 – .07 = .065, or 6.5%.
Here is the formula for Sp, the standard error of the proportion:
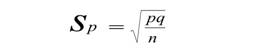
The standard error is the square root of pq/n. p is the proportion black; q is 1 – p, and n is the size of the sample, in this case the number of photographs. Multiplying .07 x .93 results in .065. Dividing by 115 results in .0006. The square root of .0006 = .025. The other proportion has no variance, so we don’t have to include it. Then we take our % difference, .065, and divide it by .025, to learn how unusual such a percentage is. The result, .065 / .025 = 2.65. Looking this up in what is called a t-table, we find that it is statistically significant at the 1% level. Such a result would happen by chance less than 1 time in 100.
If you don’t get statistical significance, you should give up and check out another company’s catalog or website, or, if you still feel it’s unduly white, then sample another edition of the catalog or website. Doing two at once roughly doubles the n, the number of photographs, which makes the standard deviation much smaller, which in turn increases the significance. This makes sense. After all, if you flipped a coin 100 times and got 60 heads, you might not be too sure that your method of flipping was biased, but if you flipped it 200 times and got 120 heads, you’d be more certain.